SciPy库简介

scipy库 中有许多科学计算常见问题的工具, 它的子模块对应于不同的应用, 比如插值, 积分, 优化, 图像处理, 统计和特殊功能等.
scipy 是Python科学计算环境的核心. 它被设计为利用 numpy 数组进行高效的运行, 从这个角度来讲, scipy和numpy是密不可分的.

SciPy结构

SciPy被组织成覆盖不同科学计算领域的子包. 下表汇总了这些信息:

子模块 描述
scipy.cluster 向量计算 / Kmeans
scipy.constants 物理和数学常量
scipy.fftpack 傅里叶变换
scipy.integrate 积分程序
scipy.interpolate 插值
scipy.io 数据输入和输出
scipy.linalg 线性代数程序
scipy.ndimage n-维图像包
scipy.odr 正交距离回归
scipy.optimize 优化
scipy.signal 信号处理
scipy.sparse 稀疏矩阵
scipy.spatial 空间数据结构和算法
scipy.special 一些特殊数学函数
scipy.stats 统计

SciPy 的子包需要分别导入, 例如:

from scipy import linalg, optimize

scipy.io 数据的输入和输出

scipy.io 最常用的主要有三个方法:

loadmat(file_name[, mdict, appendmat])

载入 MATLAB 的 .mat 文件.

savemat(file_name, mdict[, appendmat, …])

将字典和文件名保存到 MATLAB 的 .mat 文件.

whosmat(file_name[, appendmat])

列出 MATLAB 文件的一些属性.

例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np
from scipy import io as sio
temp_data = np.ones((3, 3))
sio.savemat('file.mat', {'temp_data': temp_data}) # mat格式文件输入要求格式为字典
data = sio.loadmat('file.mat', struct_as_record=True)
info = sio.whosmat('file.mat')
print(data['temp_data'])
print(info)
# 输出的结果为:
'temp_data': 
array([[0.30944564, 0.6779428 , 0.18910781, 0.16907513],
       [0.84839293, 0.65481527, 0.29616549, 0.16536131],
       [0.77168659, 0.09888839, 0.95092472, 0.46103117]])}
[('temp_data', (3, 4), 'double')]

关于 scipy.io 还有其他几种文件格式的载入与输出, 这里就不详细介绍了, 只列出来在这里, 详情可以查看 官方文档对 scipy.io 的介绍.

方法 描述
readsav(file_name[, idict, python_dict, …]) 读取 IDL 的 .sav 文件.
mminfo(source) 从类MM(Matrix Market)文件中返回大小和存储参数.
mmread(source) 读取类MM(Matrix Market)文件.
mmwrite(target, a[, comment, field, …]) 将数组a写入类MM(Matrix Market)目标.
wavfile.read(filename[, mmap]) 读取一个.wav的音轨文件.
wavfile.write(filename, rate, data) 将一个numpy数组写入.wav文件.
arff.loadarff(f) 读取一个 arff 文件.
netcdf_file(filename[, mode, mmap, version, …]) NetCDF数据的文件对象.

载入和保存text, csv或其他numpy指定类型可以使用numpy包, 详见 Python之Numpy库学习(3).

scipy.special 一些特殊数学函数

scipy.special 子包的主要特点是定义了许多数学物理的特殊函数. 可用功能包括 airy, elliptic, bessel, gamma, beta, hypergeometric, parabolic cylinder, mathieu, spheroidal wave, struve, kelvin. 还有一些低级统计函数不在 scipy.special 模块中, 因为 scipy.stats 模块为这些函数提供了更简单的接口.
这些函数中的大多数可以接受数组参数并返回数组结果, 遵循与NumPy中的其他数学函数相同的广播规则. 其中许多函数还接受复数作为输入.
下面列取几个常用的函数:

  • 贝塞尔函数, 比如scipy.special.jv() (第n个整型顺序的贝塞尔函数)
  • 椭圆函数 (scipy.special.ellipj() Jacobian椭圆函数, …)
  • Gamma 函数: scipy.special.gamma(), 也要注意 scipy.special.gammaln() 将给出更高准确数值的 Gamma的log。
  • Erf, 高斯曲线的面积：scipy.special.erf()

详情可以查看 官方文档对 scipy.special 的介绍.

scipy.linalg 线性代数操作

scipy.linalg 是基于 ATLAS, LAPACK 和 BLAS 高效底层库构建的, 它具有非常高效的线性代数操作.
如果深入研究, 所有原始的LAPACK和BLAS库都可以直接使用, 这里我们只谈一些更易于使用的接口.

scipy.linalg vs numpy.linalg

scipy.linalg 包含所有 numpy.linalg 的功能, 并在此基础上有所扩展.
在 numpy 中进行线性代数操作得到的结果为 matrix类, 虽然 matrix类 简化了一些线代操作, 但所有的操作也可以使用 2-D ndarry 实现, 而且在实际操作中也容易混淆 matrix类 和 ndarry类. 而使用 scipy.linalg 可以同时应用于 matrix类 和 2-D ndarry 类.

线代基础操作

求矩阵的逆

scipy.linalg.inv(a)

例如:

1
2
3
4
5
6
7
8
9
10
11
12
>>> import numpy as np
>>> from scipy import linalg
>>> a = np.array([[1.,2.], [3.,4.]])
>>> a
array([[1., 2.],
       [3., 4.]])
>>> linalg.inv(a)
array([[-2. ,  1. ],
       [ 1.5, -0.5]])
>>> a.dot(linalg.inv(a))
array([[1.0000000e+00, 0.0000000e+00],
       [8.8817842e-16, 1.0000000e+00]])

解线性方程组

$$\begin{cases} x + 3y + 5z = 10 \\ 2x + 5y + z = 8 \\ 2x + 3y + 8z = 3 \\ \end{cases}$$

该方程组可以转换为矩阵:

$$\begin{bmatrix} 1 & 3 & 5\\ 2 & 5 & 1 \\ 2 & 3 & 8 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 10 \\ 8 \\ 3 \end{bmatrix}$$

即可以得出:

$$\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 & 3 & 5\\ 2 & 5 & 1 \\ 2 & 3 & 8 \end{bmatrix}^{-1} \begin{bmatrix} 10 \\ 8 \\ 3 \end{bmatrix}$$

当使用 scipy.linalg 时, 就可以使计算变得非常简单.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
>>> import numpy as np
>>> from scipy import linalg
>>> a = np.array([[1,3,5], [2,5,1],[2,3,8]])
>>> a
array([[1, 3, 5],
       [2, 5, 1],
       [2, 3, 8]])
>>> b = np.array([[10], [8], [3]])
>>> b
array([[10],
       [ 8],
       [ 3]])
>>> linalg.inv(a).dot(b)  # 计算结果
array([[-9.28],
       [ 5.16],
       [ 0.76]])
>>> a.dot(linalg.inv(a).dot(b))  # 检验结果
array([[10.],
       [ 8.],
       [ 3.]])

计算行列式的值

scipy.linalg.det(a)

给定一个矩阵:

$$A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$$

计算它的行列式:

$$\mid A \mid = \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = 1 \times 4 - 2 \times 3 = -2$$

用 scipy.linalg.det() 函数计算矩阵的行列式:

1
2
3
4
5
6
7
8
>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2], [3,4]])
>>> A
array([[1, 2],
       [3, 4]])
>>> linalg.det(A)
-2.0

计算矩阵的伴随矩阵

求矩阵的伴随矩阵, 我们可以使用以下公式, 设 A 是一个行列式不为0的方阵:

$$A^* = \mid A \mid A^{-1}$$

所以, 我们可以用 linalg.det(A).dot(linalg.inv(A)) 计算矩阵 A 的伴随矩阵. 很多矩阵的计算都可以用这种思路.

求矩阵的特征值和特征向量

对于矩阵 A 若: $A \zeta = \lambda A$ , 则我们称 $\lambda$ 为 A 的特征值, $\zeta$ 为 A 的特征向量.

linalg.eig(A) 会同时 return $\lambda$ 和 $\zeta$,
linalg.eigvals(A) 只会 return $\lambda$.

例如:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[0,2,-2], [2,4,4], [-2,4,-3]])
>>> A
array([[ 0,  2, -2],
       [ 2,  4,  4],
       [-2,  4, -3]])
>>>linalg.eigvals(A)
array([-6.+0.j,  1.+0.j,  6.+0.j])
>>> linalg.eig(A)
(array([-6.+0.j,  1.+0.j,  6.+0.j]),
array([[-4.08248290e-01,  8.94427191e-01,  1.82574186e-01],
       [ 4.08248290e-01,  9.87581947e-17,  9.12870929e-01],
       [-8.16496581e-01, -4.47213595e-01,  3.65148372e-01]]))

其他矩阵操作

其他矩阵操作可以查看 官网关于linalg的文档.

scipy.fftpack 快速傅里叶变换

关于傅里叶变换, 可以参考这篇文章 如何理解傅立叶级数公式？

scipy.fftpack 模块包含了快速傅里叶变换的功能.

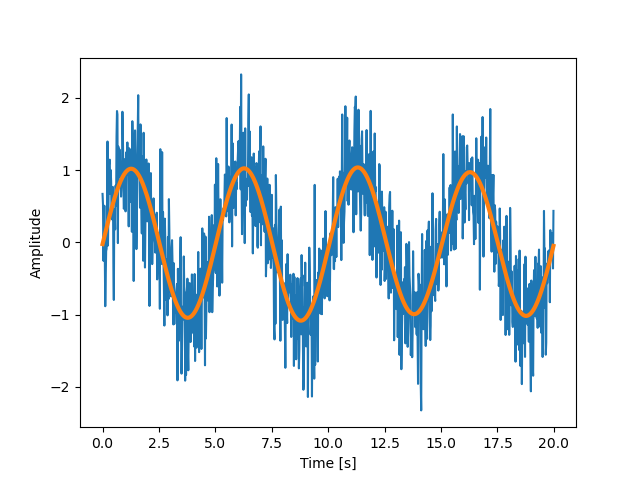
下面是一个噪声信号的例子:

1
2
3
4
5
6
import numpy as np

time_step = 0.02
period = 5.
time_vec = np.arange(0, 20, time_step)
sig = np.sin(2 * np.pi / period * time_vec) + 0.5 * np.random.randn(time_vec.size)

观察者不知道信号的频率, 只知道信号的采样间隙 sig 信号是来自真实函数的, 那么 傅里叶变换是对称的. scipy.fftpack.fftfreq() 函数会生成采样频率, scipy.fftpack.fft() 则用于进行快速傅里叶变化:

1
2
3
4
from scipy import fftpack

sample_freq = fftpack.fftfreq(sig.size, d=time_step)
sig_fft = fftpack.fft(sig)

因为生成的幂是对称的, 寻找频率只需要使用频谱为正的部分:

1
2
3
pidxs = np.where(sample_freq > 0)
freqs = sample_freq[pidxs]
power = np.abs(sig_fft)[pidxs]

信号频率可通过如下方式获得:

1
freq = freqs[power.argmax()]

滤去傅里叶变化后的信号中的高频噪声:

1
sig_fft[np.abs(sample_freq) > freq] = 0

去噪后信号可通过如下方式计算： scipy.fftpack.ifft() 方法:

1
main_sig = fftpack.ifft(sig_fft)

绘制成图:

1
2
3
4
5
6
7
8
import matplotlib.pyplot as plt

plt.figure()
plt.plot(time_vec, sig)
plt.plot(time_vec, main_sig, linewidth=3)
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.show()

scipy01

scipy.optimize 优化及拟合

scipy.optimize 模块提供了求解函数最小值, 曲线拟合等算法的实现.

求函数的最小值

定义下面的函数:

1
2
def f(x):
    return x**2 + 10*np.sin(x)

画出其图像:

1
2
3
x = np.arange(-10, 10, 0.1)
plt.plot(x, f(x))
plt.show()

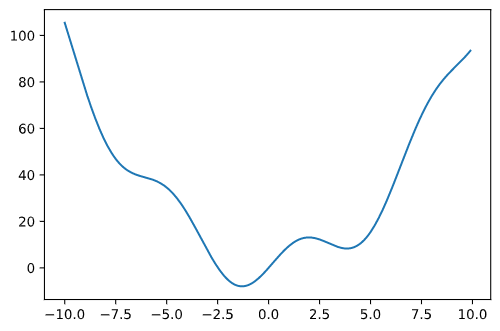
scipy02

此函数有一个全局最小值, 在 x = -1 附近, 还有一个局部最小值, 在 x = 5 附近.

一个常用的求解此函数最小值的方法是确定初始点, 然后执行梯度下降算法. BFGS算法是一个很好的适用于此的方法:

1
2
3
4
5
6
7
>>> optimize.fmin_bfgs(f, -1)
Optimization terminated successfully.
         Current function value: -7.945823
         Iterations: 3
         Function evaluations: 15
         Gradient evaluations: 5
array([-1.30644012])

这个方法的缺陷在于有时候可能会被困在一个局部最小值, 而得不到全局的最小值. 这取决与初始点的选取:

1
2
3
4
5
6
7
8
>>> optimize.fmin_bfgs(f, 5)
optimize.fmin_bfgs(f, 5)
Optimization terminated successfully.
         Current function value: 8.315586
         Iterations: 5
         Function evaluations: 18
         Gradient evaluations: 6
array([3.83746712])

如果我们不知道全局最小值的邻近数值, 就需要使用那些可以实现全局最优化的算法.比如 optimize.basinhopping() 包含一个求解局部最小值的算法和一个为该算法提供随机初始点的函数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
>>> optimize.basinhopping(f, 0)
                        fun: -7.945823375615284
 lowest_optimization_result:       fun: -7.945823375615284
 hess_inv: array([[0.08579758]])
      jac: array([0.])
  message: 'Optimization terminated successfully.'
     nfev: 15
      nit: 3
     njev: 5
   status: 0
  success: True
        x: array([-1.30644002])
                    message: ['requested number of basinhopping iterations completed successfully']
      minimization_failures: 0
                       nfev: 1497
                        nit: 100
                       njev: 499
                          x: array([-1.30644002])

另外一个可用的, 但不怎么高效的全局最优化算法是 scipy.optimize.brute().

为了找到局部最小值, 可以把变量限制在区间 (0, 10) 中, 使用 scipy.optimize.fminbound():

1
2
>>> optimize.fminbound(f, 0, 10)
3.8374671194983834

寻找函数的零点

例如, 求解 f(x) = 0 的零点, 其中 f 是我们在上面用到的函数. 可以使用 scipy.optimize.fsolve():

1
2
>>> optimize.fsolve(f, 1)
array([0.])

从上面的图像中我们可以看出函数 f 包含两个零点. 第二个零点在 x = -2.5 附近. 通过调整初始值, 我们可以找出精确解:

1
2
>>> optimize.fsolve(f, -2.5)
array([-2.47948183])

曲线拟合

假设我们现在有从函数 f 中采样得到的含有一些噪声的数据:

1
2
xdata = np.arange(-10, 10)
ydata = f(xdata) + np.random.randn(xdata.size)

我们已经知道了函数的形式是大概是:
$$ax^2 + b \sin(x) + c $$
但不知道每一项系数的大小. 我们可以使用最小二乘算法来进行曲线拟合得到系数的值. 首先定义需要进行拟合的函数:

1
2
def f2(x, a, b, c):
     return a*x**2 + b*np.sin(x) + c

接着使用 scipy.optimize.curve_fit() 来求解 a, b, c:

1
2
3
>>> params, params_covariance = optimize.curve_fit(f2, xdata, ydata, guess)
>>>params
array([ 0.98955234, 10.0579609 ,  0.15395008])

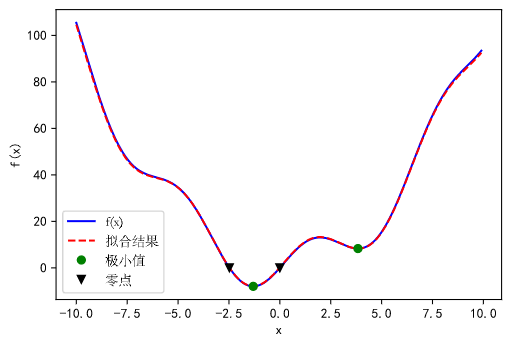
现在我们已经找到了函数 f 的最小值和零点, 并且对采自这个函数的数据进行了曲线拟合的实验. 我们可以把所有的结果呈现在同一张图像上: 

1
2
3
4
5
6
7
8
9
10
11
fig, ax = plt.subplots()
plt.rcParams['axes.unicode_minus']=False  # 解决负号乱码问题
ax.plot(x, f(x), 'b-', label="f(x)")
ax.plot(x, f2(x, *params), 'r--', label="拟合结果", )
xmins = np.array([optimize.fmin_bfgs(f, -1), optimize.fmin_bfgs(f, 5)])
ax.plot(xmins, f(xmins), 'go', label="极小值")
roots = np.array([optimize.fsolve(f, 1), optimize.fsolve(f, -2.5)])
ax.plot(roots, f(roots), 'kv', label="零点")
ax.legend(prop={'family' : 'STSong', 'size' : 10})
ax.set_xlabel('x')
ax.set_ylabel('f(x)')

scipy03

参考文献

1. SciPy — SciPy v1.4.1 Reference Guide
2. Varoquaux, Gaël, et al. Scipy Lecture Notes. 2015.