使用Python进行统计假设检验

简单说明

R是一个专门用于统计分析的编程语言, Python则是一个通用编程语言, 以统计相关的模块的方式进行统计分析. R比Python有更多的统计功能, 以及对统计更亲切的语法. 但无论如何, 当建立更复杂的工作流, 如与图像分析, 文本挖掘或者物理实验控制集成时, Python的通用性与相关模块就成了无价的财富.

统计假设检验

假设检验的基本思想是“小概率事件”原理, 其统计推断方法是带有某种概率性质的反证法. 小概率思想是指小概率事件在一次试验中基本上不会发生. 反证法思想是先提出检验假设, 再用适当的统计方法, 利用小概率原理, 确定假设是否成立. 即为了检验一个假设$H_0$是否正确, 首先假定该假设$H_0$正确, 然后根据样本对假设$H_0$做出接受或拒绝的决策. 如果样本观察值导致了“小概率事件”发生, 就应拒绝假设$H_0$, 否则应接受假设$H_0$.

基本步骤

1. 提出检验假设又称无效假设, 符号是$H_0$; 备择假设的符号是$H_1$.
   $H_0$: 样本与总体或样本与样本间的差异是由抽样误差引起的;
   $H_1$: 样本与总体或样本与样本间存在本质差异;
   预先设定的检验水准为0.05; 当检验假设为真, 但被错误地拒绝的概率, 记作$\alpha$, 通常取$\alpha=0.05$或$\alpha=0.01$.
2. 选定统计方法, 由样本观察值按相应的公式计算出统计量的大小, 如$X_2$值, t值等. 根据资料的类型和特点, 可分别选用Z检验, T检验, 秩和检验和卡方检验等.
3. 根据统计量的大小及其分布确定检验假设成立的可能性P的大小并判断结果. 若 $P>\alpha$, 结论为按α所取水准不显著, 不拒绝H0, 即认为差别很可能是由于抽样误差造成的, 在统计上不成立; 如果 $P≤\alpha$, 结论为按所取α水准显著, 拒绝H0, 接受H1, 则认为此差别不大可能仅由抽样误差所致, 很可能是实验因素不同造成的, 故在统计上成立. P值的大小一般可通过查阅相应的界值表得到.
4. 注意问题:

• 作假设检验之前, 应注意资料本身是否有可比性.
• 当差别有统计学意义时应注意这样的差别在实际应用中有无意义.
• 根据资料类型和特点选用正确的假设检验方法.
• 根据专业及经验确定是选用单侧检验还是双侧检验.
• 判断结论时不能绝对化, 应注意无论接受或拒绝检验假设, 都有判断错误的可能性.

t检验

t检验, 亦称student t检验(Student’s t test), 主要用于样本含量较小(例如 $n < 30$), 总体标准差$\delta$未知的正态分布. t检验是用t分布理论来推论差异发生的概率, 从而比较两个平均数的差异是否显著.

Python实现单样本t检验

单样本t检验用于比较样本数据与一个特定数值之间是否的差异情况.

假设有这样一组数据(某省各城市的平均月工资):

City	AverageMonthlySalary
A	9000
B	8800
C	8900
D	7500
E	8500
F	7600
G	8000
H	7800
I	8200
J	8300

我们要检验其与全国月平均工资8829元是否存在显著差异.

假设:
$H_0$: 该省各城市的平均月工资与全国月平均工资相同
$H_1$: 该省各城市的平均月工资与全国月平均工资不同

选用双侧检验, 选用$\alpha=0.01$的统计显著水平

导入数据

>>> import pandas
>>> data = pandas.read_csv('salary.csv')
>>> data['AverageMonthlySalary']
0    9000
1    8800
2    8900
3    7500
4    8500
5    7600
6    8000
7    7800
8    8200
9    8300
Name: AverageMonthlySalary, dtype: int64

数据可视化

import matplotlib.pyplot as plt

fig, ax = plt.subplots()
ax.bar(data['City'],data['AverageMonthlySalary'])
ax.set_xlabel('City')
ax.set_ylabel('Average Monthly Salary')

输出结果如图:

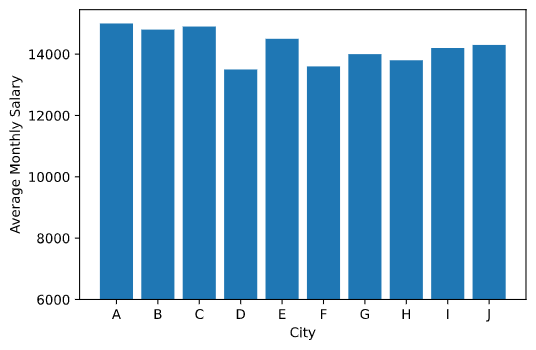
单样本t检验

scipy.stats.ttest_1samp(a, popmean) 检验是样本数据与一个特定数值之间是否的差异情况. 它返回t值与p值.

>>> from scipy import stats
>>> stats.ttest_1samp(data['AverageMonthlySalary'], 8829)
Ttest_1sampResult(statistic=-3.3451302386251056, pvalue=0.008589795741200947)

可以看到 $p<0.01$, 说明统计结果达到显著意义, 接受$H_1$, 在$\alpha=0.01$的统计显著水平下该省各城市的平均月工资与全国月平均工资不同.

Python实现独立样本t检验

独立样本t检验用于分析定类数据(X)与定量数据(Y)之间的差异情况.

假设有这样一组数据(某公司男女身高数据):

Name	Gender	Height
A	Female	164
B	Female	160
C	Male	166
D	Male	175
E	Female	170
F	Male	183
G	Male	176
H	Female	156
I	Male	168
J	Male	177
k	Female	161

我们要检验该公司男性与女性的身高是否存在显著差异.

假设:
$H_0$: 该公司男性与女性的身高不存在显著差异
$H_1$: 该公司男性与女性的身高存在显著差异

选用双侧检验, 选用$\alpha=0.01$的统计显著水平

导入数据

>>> import pandas
>>> data = pandas.read_csv('salary.csv')
>>> data
    Name	Gender	Height
0	A	Female	164
1	B	Female	160
2	C	Male	166
3	D	Male	175
4	E	Female	170
5	F	Male	183
6	G	Male	176
7	H	Female	156
8	I	Male	168
9	J	Male	177
10	k	Female	161

数据可视化

import matplotlib.pyplot as plt

fig, axs = plt.subplots(1,2)
data_male = data[data['Gender'] == 'Male']
data_female = data[data['Gender'] == 'Female']
axs[0].bar(data_male['Name'], data_male['Height'], color='b', label='Male')
axs[1].bar(data_female['Name'], data_female['Height'], color='r', label='Female')
for ax in axs:
    ax.set_xlabel('Name')
    ax.set_ylabel('Height(cm)')
    ax.legend()

输出结果如图:

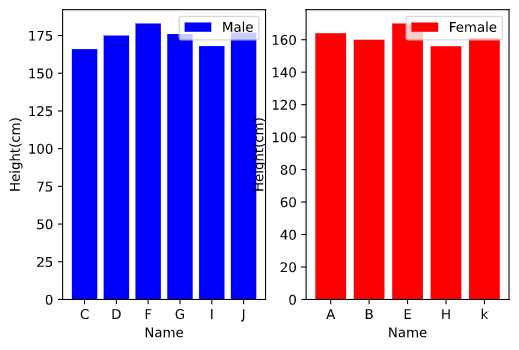
独立样本t检验

scipy.stats.ttest_ind(a, b, equal_var) 检验两样本之间差异的显著性. 它返回t值与p值. equal_var参数为bool类型, 是否等方差.

当不确定两总体方差是否相等时, 应先利用levene检验, 检验两总体是否具有方差齐性：

>>> from scipy import stats
>>> stats.levene(data_male['Height'], data_female['Height'])
LeveneResult(statistic=0.14705486820871433, pvalue=0.7102672800386702)

p值远大于0.05, 认为两总体具有方差齐性.
如果两总体不具有方差齐性, 需要将equal_val参数设定为False.

>>> from scipy import stats
>>> stats.ttest_ind(data_male['Height'], data_female['Height'])
Ttest_indResult(statistic=3.4023893451544494, pvalue=0.007843582968708454)

可以看到 $p<0.05$, 说明统计结果达到显著意义, 接受$H_1$, 在$\alpha=0.01$的统计显著水平下该公司男性与女性的身高存在显著差异.

Python实现配对样本t检验

配对样本t检验用于分析配对定量数据之间的差异对比关系. 与独立样本t检验相比, 配对样本t检验要求样本是配对的. 两个样本的样本量要相同, 样本先后的顺序是一一对应的.

假设有这样一组数据(某实验的前后数据):

Test	Before	After
1	30	38
2	35	36
3	33	38
4	32	40
5	29	33
6	32	37
7	35	39

我们要检验该实验是否对数据大小存在显著影响.

假设:
$H_0$: 该实验对数据大小不存在显著影响
$H_1$: 该实验对数据大小存在显著影响

选用双侧检验, 选用$\alpha=0.01$的统计显著水平

导入数据

>>> import pandas
>>> data = pandas.read_csv('test.csv')
>>> data
    Test    Before	After
0	1	30	38
1	2	35	36
2	3	33	38
3	4	32	40
4	5	29	33
5	6	32	37
6	7	35	39

数据可视化

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
bar_width = 0.35
index = np.arange(len(data))
ax.bar(index, data['Before'] , bar_width, label='Before')
ax.bar(index + bar_width, data['After'], bar_width, label='After')
ax.set_xticks(index + bar_width / 2)
ax.set_xticklabels(data['Test'])
ax.legend()

输出结果如图:

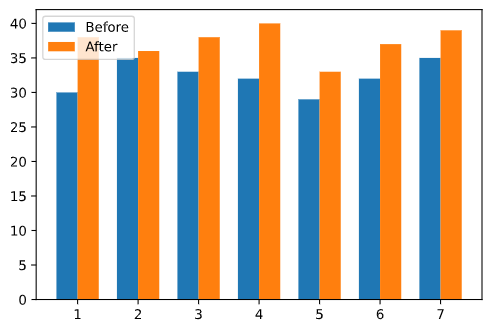
配对样本t检验

scipy.stats.ttest_rel(a, b) 检验不同条件是否对数据有显著影响. 它返回t值与p值.

>>> from scipy import stats
>>> stats.ttest_rel(data['Before'], data['After'])
Ttest_relResult(statistic=-5.400617248673217, pvalue=0.0016629169382403571)

可以看到 $p<0.01$, 说明统计结果达到显著意义, 接受$H_1$, 在$\alpha=0.01$的统计显著水平下该实验对数据大小存在显著影响.

卡方检验

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度, 实际观测值与理论推断值之间的偏离程度就决定卡方值的大小, 如果卡方值越大, 二者偏差程度越大; 反之, 二者偏差越小; 若两个值完全相等时, 卡方值就为0, 表明理论值完全符合.

Python实现卡方适合度检验

实际执行多项式试验而得到的观察次数, 与虚无假设的期望次数相比较, 称为卡方适度检验, 即在于检验二者接近的程度, 利用样本数据以检验总体分布是否为某一特定分布的统计方法.

假设有这样一组数据(掷120次骰子的结果):

Point	Obs	Exp
1	22	20
2	19	20
3	23	20
4	17	20
5	20	20
6	19	20

假设:
$H_0$: 观察分布等于期望分布
$H_1$: 观察分布不等于期望分布

选用$\alpha=0.05$的统计显著水平

导入数据

>>> import pandas
>>> data = pandas.read_csv('point.csv')
>>> data
    Point   Obs Exp
0	1	22	20
1	2	19	20
2	3	23	20
3	4	17	20
4	5	20	20
5	6	19	20

数据可视化

import matplotlib.pyplot as plt

fig, ax = plt.subplots()
bar_width = 0.35
ax.bar(data['Point'], data['Obs'] , bar_width, label='Observe')
ax.bar(data['Point'], data['Exp'], bar_width, fill=False, label='Expectation')
ax.legend()

输出结果如图:

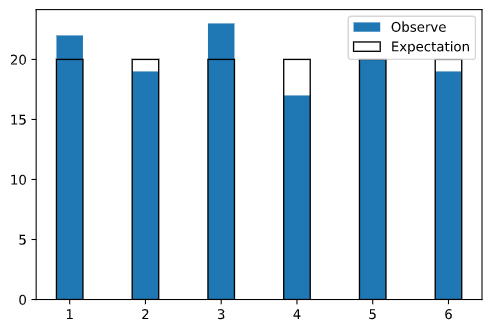
卡方适合度检验

scipy.stats.chisquare(f_obs, f_exp=None) 检验统计样本的实际观测值与理论推断值之间的偏离程度. 它返回卡方统计量与p值.

>>> from scipy import stats
>>> stats.chisquare(data['Obs'], data['Exp'])
Power_divergenceResult(statistic=1.2, pvalue=0.9448773650021219)

附卡方鉴定表:

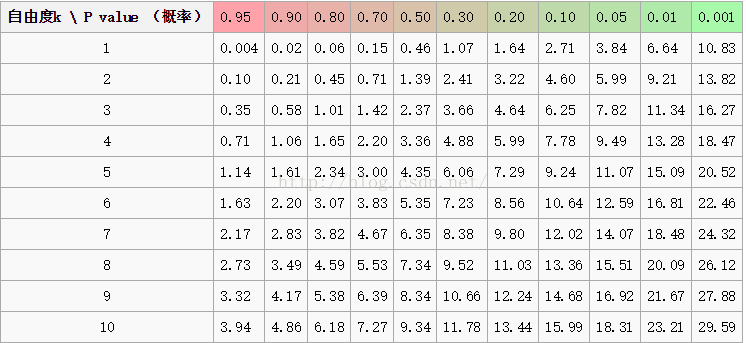
该样例自由度为$(6-1)\times(2-1)=5$, $\alpha=0.05$, 查表可得临界值为11.07, 可以看到 $1.2<11.07$, 即统计量小于临界值, 故差异不显著, 接受$H_0$, 在$\alpha=0.05$的统计显著水平下观察分布等于期望分布.

Python实现卡方独立性检验

卡方独立性检验是用来检验两个属性间是否独立. 一个变量作为行, 另一个变量作为列.

举个例子:
检验满足感和年龄之间是否独立, 下面是一组虚构的满足感和年龄之间的数据:

Satisfaction\Age	Male	Female
Yes	42	36
No	87	37
Don’t know	20	16

假设:
$H_0$: 满足感和性别之间相互独立
$H_1$: 满足感和性别之间相互关联

选用$\alpha=0.05$的统计显著水平

导入数据

>>> import pandas
>>> data = pandas.read_csv('satisfaction_sex.csv')
>>> data
	Satisfaction\Sex	Male	Female
0	Yes	42	36
1	No	87	37
2	Don't know	20	16

数据可视化

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
bar_width = 0.25
index = np.arange(2)
ax.bar(index, data.values[0][1:] , bar_width, label='Yes')
ax.bar(index + bar_width, data.values[1][1:], bar_width, label='No')
ax.bar(index + bar_width + bar_width, data.values[2][1:] , bar_width, label="Don't konw")
ax.set_xticks(index + bar_width)
ax.set_xticklabels(data.columns[1:])
ax.legend()

输出结果如图:

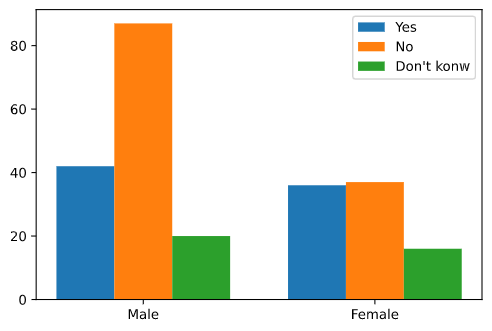
卡方独立性检验

scipy.stats.chi2_contingency(observed) 对横竖两个列表的独立性进行检验. 它返回卡方统计量, p值, 自由度和预期频率.

>>> from scipy import stats
>>> stats.chi2_contingency(data)
(6.344442816506179,
 0.0419103943243306,
 2,
 array([[48.83193277, 29.16806723],
        [77.6302521 , 46.3697479 ],
        [22.53781513, 13.46218487]]))

该样例自由度为$(3-1)\times(2-1)=2$, $\alpha=0.05$, 查表可得临界值为5.99, 可以看到 $6.34>5.99$, 即统计量大于临界值, 故差异显著, 拒绝$H_0$, 接受$$H_1$, 在$\alpha=0.05$的统计显著水平下满足感和性别之间相互联系.

Python实现卡方统一性检验

检验两个或两个以上总体的某一特性分布, 也就是各“类别”的比例是否统一或相近, 一般称为卡方统一性检验或者卡方同质性检验.

举个例子:
下面是A, B两个地区对满意度调查问卷的结果:

Satisfaction	A	B
5	25	23
4	20	22
3	35	32
2	12	14
1	8	9

假设:
$H_0$: A, B两地区的满意度比例相同
$H_1$: A, B两地区的满意度比例不同

选用$\alpha=0.05$的统计显著水平

导入数据

>>> import pandas
>>> data = pandas.read_csv('satisfaction_area.csv')
>>> data
    Satisfaction	A	B
0	5	25	23
1	4	20	22
2	3	35	32
3	2	12	14
4	1	8	9

数据可视化

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
bar_width = 0.35
index = np.arange(5)
ax.bar(index, data['A'] , bar_width, label='A')
ax.bar(index + bar_width, data['B'], bar_width, label='B')
ax.set_xticks(index + bar_width/2)
ax.set_xticklabels(data['Satisfaction'])
ax.legend()

输出结果如图:

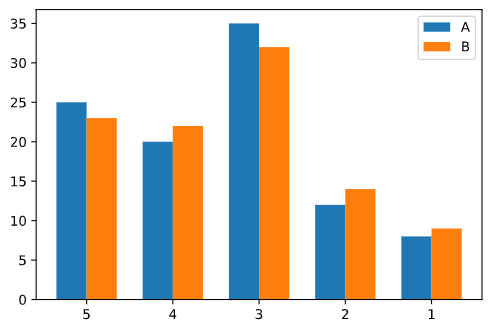
卡方统一性检验

这里用的方法和卡方适合度检验一样, 就不再详细描述了, 直接展示代码:

>>> from scipy import stats
>>> stats.chisquare(data['A'], data['B'])
Power_divergenceResult(statistic=1.0338066221218394, pvalue=0.9046272037861618)

该样例自由度为$(5-1)\times(2-1)=4$, $\alpha=0.05$, 查表可得临界值为9.49, 可以看到 $1.03<9.49$, 即统计量小于临界值, 故差异不显著, 接受$H_0$, 在$\alpha=0.05$的统计显著水平下A, B两地区的满意度比例相同.

方差分析

方差分析(ANOVA)又称”变异数分析”或”F检验”, 是由R.A.Fister发明的, 用于两个及两个以上样本均数差别的显著性检验.

Python实现单因素方差分析

单因素方差分析(One Way ANOVA)是指对单因素试验结果进行分析, 检验因素对试验结果有无显著性影响的方法.

例如:
将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象, 以致减少了药效. 下表列出了5种常用的抗生素注入到牛的体内时, 抗生素与血浆蛋白质结合的百分比. 现需要在显著性水平$\alpha = 0.05$下检验这些百分比的均值有无显著的差异. 设各总体服从正态分布, 且方差相同.

青霉素	四环素	链霉	红霉素	氯霉素
29.6	27.3	5.8	21.6	29.2
24.3	32.6	6.2	17.4	32.8
28.5	30.8	11.0	18.3	25.0
32.0	34.8	8.3	19.0	24.2

　在这里, 试验的指标是抗生素与血浆蛋白质结合的百分比, 抗生素为因素, 不同的5种抗生素就是这个因素的五个不同的水平. 假定除抗生素这一因素外, 其余的一切条件都相同. 这就是单因素试验. 试验的目的是要考察这些抗生素与血浆蛋白质结合的百分比的均值有无显著的差异. 即考察抗生素这一因素对这些百分比有无显著影响. 这就是一个典型的单因素试验的方差分析问题.

假设:
$H_0$: 各个总体的均值相等
$H_1$: 各个总体的均值不全相等

导入数据

>>> import pandas
>>> data = pandas.read_csv('medicine.csv')
>>> data
    Pen	Tet	Str	Ery	Chl
0	29.6	27.3	5.8	21.6	29.2
1	24.3	32.6	6.2	17.4	32.8
2	28.5	30.8	11.0	18.3	25.0
3	32.0	34.8	8.3	19.0	24.2

数据可视化

import matplotlib.pyplot as plt

fig, ax = plt.subplots()
ax.boxplot([data['Pen'], data['Tet'], data['Str'], data['Ery'], data['Chl']])
ax.set_xticklabels(['青霉素', '四环素', '链霉', '红霉素', '氯霉素'], fontproperties = 'STSong')

输出结果如图:

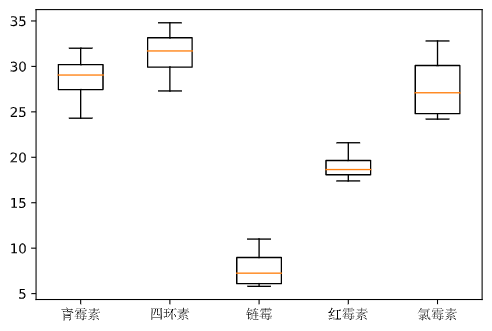
单因素方差分析

scipy.stats.f_oneway(*args) 单因素方差分析, 返回f值和p值.

或者:

statsmodels.stats.anova.anova_lm(*args) 一个或多个因素方差分析, 返回方差分析表

>>> from scipy import stats
>>> stats.f_oneway(data['Pen'], data['Tet'], data['Str'], data['Ery'], data['Chl'])
F_onewayResult(statistic=40.88487732150424, pvalue=6.739775552625242e-08)

或者:

>>> from statsmodels.formula.api import ols
>>> from statsmodels.stats.anova import anova_lm
>>> data_melt = data.melt() # 将数据翻转
>>> data_melt
	variable	value
0	Pen	29.6
1	Pen	24.3
2	Pen	28.5
3	Pen	32.0
4	Tet	27.3
5	Tet	32.6
6	Tet	30.8
7	Tet	34.8
8	Str	5.8
9	Str	6.2
10	Str	11.0
11	Str	8.3
12	Ery	21.6
13	Ery	17.4
14	Ery	18.3
15	Ery	19.0
16	Chl	29.2
17	Chl	32.8
18	Chl	25.0
19	Chl	24.2
>>> formula = 'value~C(variable)'
>>> model = ols(formula=formula, data=data_melt).fit()
>>> anova_lm(model)
    df	sum_sq	mean_sq	F	PR(>F)
C(variable)	4.0	1480.8230	370.205750	40.884877	6.739776e-08
Residual	15.0	135.8225	9.054833	NaN	NaN

$p=6.739776e-08$小于0.05, 故拒绝$H_0$, 接受$H_1$, 即在$\alpha=0.05$的统计显著水平下, 各个总体的均值不全相等.

Python实现多因素方差分析

多因素方差分析法是一种统计分析方法是用来分析两个或以上因素的不同水平对结果是否有显著影响, 以及两因素之间是否存在交互效应.

例如:
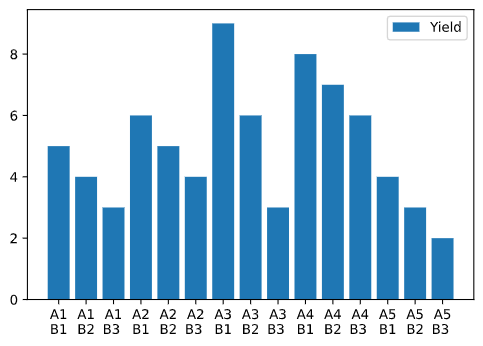
以下是虚构的施不同肥料比例对产量的影响:

N/P	B1	B2	B3
A1	5	4	3
A2	6	5	4
A3	9	6	3
A4	8	7	6
A5	4	3	2

假设:

• 要说明性别有无显著影响, 就是检验如下假设:
  $H_0$: 施N肥不同水平下观测变量的总体均值无显著差异.
  $H_1$: 施N肥不同水平下观测变量的总体均值存在显著差异.

• 要说明年龄有无显著影响, 就是检验如下假设:
  $H_0$: 施P肥不同水平下观测变量的总体均值无显著差异.
  $H_1$: 施P肥不同水平下观测变量的总体均值存在显著差异.

• 在有交互效应的双因素方差中, 要说明两个因素的交互效应是否显著, 还要检验第三组零假设和备择假设:
  $H_0$: 施N肥和施P肥交互效应对观测变量的总体均值无显著差异.
  $H_1$: 施N肥和施P肥交互效应对观测变量的总体均值存在显著差异.

导入数据

>>> import pandas
>>> data = pandas.read_csv('fertilization.csv')
>>> data
    N/P	B1	B2	B3
0	A1	5	4	3
1	A2	6	5	4
2	A3	9	6	3
3	A4	8	7	6
4	A5	4	3	2

数据可视化

import matplotlib.pyplot as plt
import numpy as np

data = data.set_index('N/P').stack().reset_index()  # 将数据整理成行
data.columns=['N', 'P', 'Yield']  # 重命名列名

fig, ax = plt.subplots()
index = np.arange(15)
ax.bar(index , data['Yield'], label='Yield')
ax.set_xticks(index)
index_label = []
for i in range(15):
    index_label.append(data.loc[i]['N'] +'\n'+ data.loc[i]['P'])
ax.set_xticklabels(index_label)
ax.legend()

输出结果如图:

多因素方差分析

statsmodels.stats.anova.anova_lm(*args) 一个或多个因素方差分析, 返回方差分析表

>>> from statsmodels.formula.api import ols
>>> from statsmodels.stats.anova import anova_lm
>>> data
N	P	Yield
0	A1	B1	5
1	A1	B2	4
2	A1	B3	3
3	A2	B1	6
4	A2	B2	5
5	A2	B3	4
6	A3	B1	9
7	A3	B2	6
8	A3	B3	3
9	A4	B1	8
10	A4	B2	7
11	A4	B3	6
12	A5	B1	4
13	A5	B2	3
14	A5	B3	2
>>> formula = 'Yield ~ N + P'
>>> model = ols(formula=formula, data=data).fit()
>>> anova_lm(model)
	df	sum_sq	mean_sq	F	PR(>F)
N	4.0	30.0	7.5	9.375	0.004106
P	2.0	19.6	9.8	12.250	0.003671
Residual	8.0	6.4	0.8	NaN	NaN

N $p=0.0041$, P $p=0.0037$均小于0.05, 故均拒绝$H_0$, 接受$H_1$, 即在$\alpha=0.05$的统计显著水平下, N, P不同水平下观测变量的总体均值存在显著差异.

对于二因素有交互的方差分析, 还应在 formula 后加入A:B 以便显示交互结果.

后记

写了这么多, 自己等于是把从前丢掉的重新又给捡起来, 后悔当初没认真学, 现在查个资料都难. 难免有很多错误, 希望大家不吝指出.

参考文献

1. 三种T检验的详细区分
2. t检验_百度百科
3. 卡方检验 - MBA智库百科
4. 单因素方差分析 - MBA智库百科
5. t分布，卡方x分布，F分布 - Thinkando - 博客园
6. 假设检验_百度百科